原始题目：剑指 Offer 38. 字符串的排列 (opens new window)

解题思路：

对于长度为 $N$ 的不重复字符串，它的排列方案有 $N!$ 种。

可以采取字符交换的方式，先固定第 $1$ 位、再固定第 $2$ 位、……、最后固定第 $n$ 位。如下图：

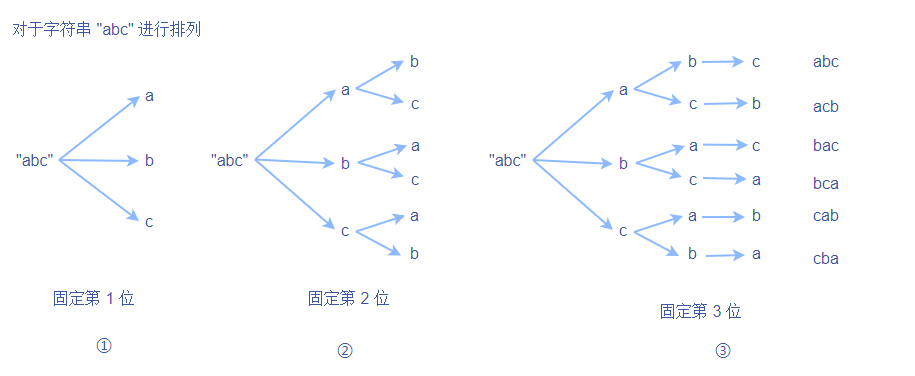
以 "acb" 为例子，来讲述生成过程的思路。

1. 初始时字符数组为 {'a', 'b', 'c'} ，且所有的交换都是和本身以及后面的元素交换。
2. 固定第 $1$ 位，第 $1$ 位固定为 a（代码中就是 a 和 a 位置交换），剩下的可操作字符串就是 "bc"。
3. 固定第 $2$ 位，第 $2$ 位可以固定为 b 或者 c (代码中就是 b 和 b 交换位置，或者 b 和 c 交换位置)
   1. 假设 b 和 c 交换位置，那么第二位固定为 c，剩下的可操作字符串就是 "b"。
4. 固定第 $3$ 位，第 $3$ 位只剩下一个 b 可以选择，因此整个过程结束。此时字符数组的内容就是 {'a', 'c', 'b'} 。

**如果后面的元素有重复的话，就不需要交换了，因为会产生一个重复的结果。**因此碰到重复的元素，要跳过。

这个过程实际是一个深度优先搜索+剪枝法的结合

dfs函数

**传递参数：**当前固定位 $x$。

**终止条件：**当 $x = len(c) - 1$ 时，表示 $x$已经时最后一个字符了，只有一种情况，因此将组合 $c$ 转化成字符串加入 $ans$ 列表。

递推工作：

1. 初始化一个集合 $set$，用来排除重复的字符串。
2. 将第 $x$ 位的字符与 $i$ $\in$ $[x, len(c) - 1]$ 的字符分别交换，然后进入下一层递归
   1. 剪枝：如果 $c[i]$ 在 $set$ 中，代表这个字符已经交换过了，跳过这个字符。
   2. 交换字符：将 $x$ 位置和 $i$ 位置的字符进行交换
   3. 下一层递归：将当前位置 $x + 1$ 作为参数，传递给下一层递归。
   4. 还原字符：将 $x$ 位置和 $i$ 位置的字符再进行一次交换。
   5. 将 $c[i]$ 加入到 $set$ 中，方便后面的剪枝。

代码：

List<String> ans = new ArrayList<>();
char[] chars;

public String[] permutation(String s) {
    chars = s.toCharArray();
    dfs(0);
    return ans.toArray(new String[0]);
}

private void dfs(int x) {
    if (x == chars.length) {
        ans.add(new String(chars));
        return;
    }
    HashSet<Character> set = new HashSet<>();
    for (int i = x; i < chars.length; i++) {
        if (set.contains(chars[i])) {
            // 剪枝
            continue;
        }
        swap(i, x);
        dfs(x + 1);
        swap(i, x);
        set.add(chars[i]);
    }
}

private void swap(int i, int j) {
    char tmp = chars[i];
    chars[i] = chars[j];
    chars[j] = tmp;
}

复杂度分析

• 时间复杂度$O(N!N)$：$N$ 为字符串的长度，最坏情况下，所有字符都不相同，需要生成 $N!$ 个结果，每个结果都需要使用 $O(N)$ 的时间来拼接字符串。
• 空间复杂度$O(N^2)$：$N$ 为字符串的长度，整个过程累计递归栈空间为 $O(N)$；每层递归中辅助集合存储的字符串数量最多为 $N + (N-1) + (N-2) + ... + 2 + 1 = \frac{(N+1)N}{2}$，及占用 $O(N^2)$ 的空间。